48++ All Basic Integration Formulas Pdf

All Basic Integration Formulas Pdf. 2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: Linearity af(x)+bg(x)dx = a f(x)dx+b g(x)dx substitution f(w(x.

We used basic integration rules to solve problems. Using the fundamental theorems of integrals, there are generalized results obtained which are remembered as integration formulas in indefinite integration. The important thing to remember is that you must eliminate all instances of the original variable x.

apprenticeship levy allowance 2018 50 200mm lens aspirateur robot laveur one aluminium angle sizes

6808feb13a70e0d27756a82c092f1d73.jpg 537×727 pixels

2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: Because we have an indefinite ∫ x n.dx = x (n + 1) / (n + 1)+ c. Integration formulas z dx = x+c (1) z xn dx = xn+1 n+1 +c (2) z dx x = ln|x|+c (3) z ex dx = ex +c (4) z ax dx = 1 lna ax +c (5) z lnxdx = xlnx−x+c (6) z sinxdx = −cosx+c (7) z cosxdx = sinx+c (8) z tanxdx = −ln|cosx|+c (9) z cotxdx = ln|sinx|+c (10) z secxdx = ln|secx+tanx|+c (11) z cscxdx = −ln |x+cot +c (12) z sec2 xdx = tanx+c (13) z csc2 xdx = −cotx+c (14) z

The reverse process is to obtain the function f(x) from knowledge of its derivative. We identified it from honorable source. Using the fundamental theorems of integrals, there are generalized results obtained which are remembered as integration formulas in indefinite integration. ˇ 180 = t x) t= ˇx 180 and x= 180 t ˇ half angle formulas sin = r 1.

Integration formulas z dx = x+c (1) z xn dx = xn+1 n+1 +c (2) z dx x = ln|x|+c (3) z ex dx = ex +c (4) z ax dx = 1 lna ax +c (5) z lnxdx = xlnx−x+c (6) z sinxdx = −cosx+c (7) z cosxdx = sinx+c (8) z tanxdx = −ln|cosx|+c (9) z cotxdx =.

We solved general differential equations. Using the fundamental theorems of integrals, there are generalized results obtained which are remembered as integration formulas in indefinite integration. Z dx x = ln|x|+c 4. Example8.1.1 evaluate z (ax+b)ndx, assuming that a and b are constants, a 6= 0, and n is a positive integer. Formula to convert into an integral involving trig functions.

Linearity af(x)+bg(x)dx = a f(x)dx+b g(x)dx substitution f(w(x. Z sinxdx = −cosx+c 6. If n6= 1 lnjxj+ c; Because we have an indefinite ∫cos x = sin x + c.

Multimedia link the following applet shows a. Z sinxdx = −cosx+c 6. ˇ 180 = t x) t= ˇx 180 and x= 180 t ˇ half angle formulas sin = r 1 cos(2 ) 2 cos = r 1 + cos(2 ) 2 tan = s 1 cos(2 ) 1 + cos(2 ) sum and di erence formulas sin( ).

∫1/x.dx = log|x| + c. Basic properties/formulas/rules d (cf x cf x( )) ( ) dx = ′ , is any constant.c (xgxf xgf x( )± =±( ))′ ′′( ) ( ) d (x nxnn) 1 dx = −, n is any number. Formula to convert into an integral involving trig functions. Z sinxdx = −cosx+c 6. ∫cos x =.

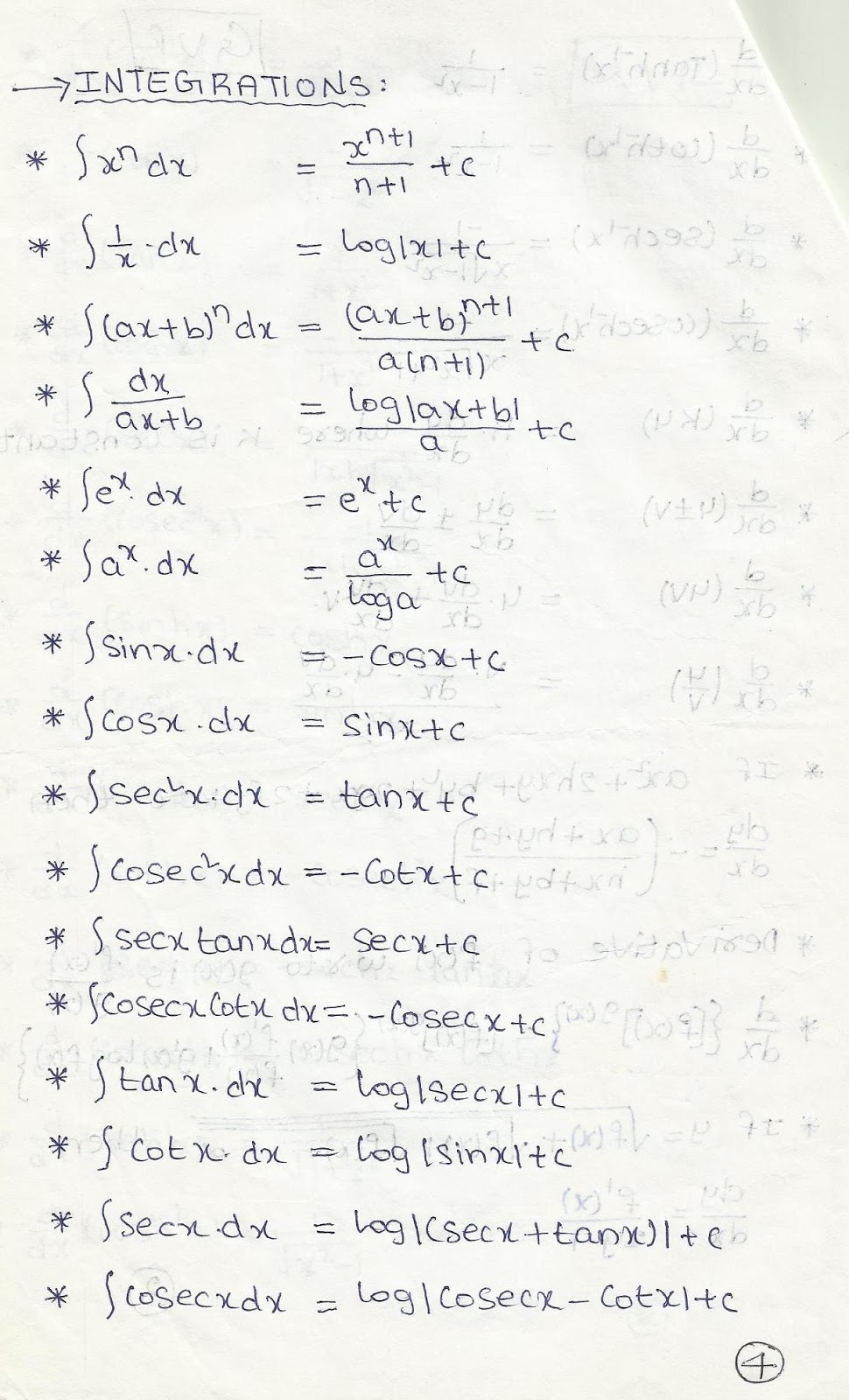
Z dx x = ln|x|+c 4. Integration formulas the following list provides some of the rules for finding integrals and a few of the common antiderivatives of functions. Linearity af(x)+bg(x)dx = a f(x)dx+b g(x)dx substitution f(w(x. Z [f(x)±g(x)] dx = z f(x)dx± z g(x)dx 2. If f and g are functions of x such that g’(x) = f(x) then, ∫.